前回の記事では、収益還元法が日本に定着してきた歴史を振り返り、現在における収益還元法の位置づけを解説いたしました。
今回から、いよいよ収益還元法の中身を解説していきます。
まず、収益還元法の基本系を押さえた上で、各パーツである収益と利回りについて順次解説していきたいと思います。
今回は次のステップに進むための基礎中の基礎なので、中級者以上の方は流し読みしていただけますと幸いです。
収益還元法とはそもそも
収益還元法はその言葉の通り、収益を資本還元する方法であります。
収益還元法(直接還元法)の公式は単純です。
還元利回りを英語では、Capitalization Rateといいます。
CapRate(キャップレート)と呼ばれたり、単にCap(キャップ)と略したりしますね。
収益還元法はアメリカからの輸入モノなので、逆に、Capitalization Rateの日本語訳が還元利回りといったほうが正しい理解です。
Capitalization Rateとは、直訳すれば、「資本還元レート」となり、収益を還元、つまり割り算することにより価格を求める際に用いられるレートです。
そしてこの収益は、年間の収入から年間の経費を控除したものであり、還元利回りは年利となります。
簡単ですね。以上!
となればいいのですが、奥が深いのが収益還元法です。
元本と果実の関係
銀行預金におカネを預けると利子がつきますね。
株に投資すれば、配当を受けられますね。
これらの預金や株などに投資する際のおカネを元本(がんぽん)と言います。
ということになりますね。
例えば、配当利回り2%の金融商品があったとすれば、100万円を投資すれば、
100万円×2%=2万円が毎年の配当として得られることになります。
この数式を逆転させれば、
となりますね。
不動産の価格の公式と同じ構造ですね。
これは一般に、「元本と果実の関係」と言われています。
このように、価格と利回りと収益のトライアングル関係が成り立つということを覚えておいてください。
割引現在価値
以上の解説は、元本と果実の関係から導き出した収益還元法の公式ですが、投資の世界で重要な割引現在価値という概念をここで解説していきたいと思います。
この考え方は、後で解説するDCF法の理解の基礎となるので非常に重要です。
例えば、5%の配当が付く金融商品があったとしましょう。
この金融商品を100で買うと1年後には配当込みで価格は105になりますね。
そして、この105を再運用すると105×5%の=5.25円の配当が得られることになります。
このように当初の元金に利息・配当金に加えて再運用していくことを「複利」による運用と言います。
そしてこの商品を引き出すことなく再運用を繰り返していき10年間運用した場合の運用収支は次の通りになります。
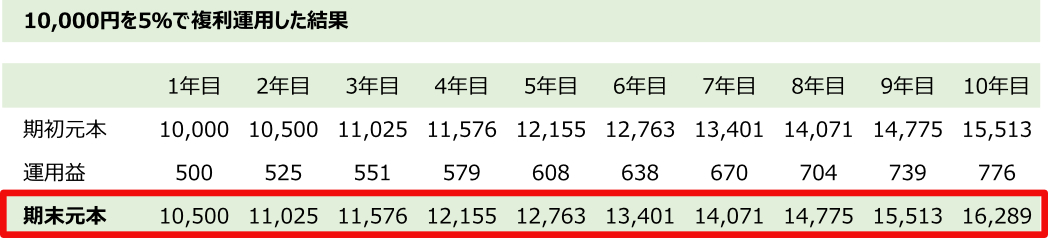
10,000円を5%の複利で運用し続けると、10年後には16,289円と当初の元金が1.6倍になりますね。
アインシュタインが、「複利は人類最大の発明」とまでいったパワーが感じられます。
さて、ここからが不動産評価では重要です。
割引現在価値とは?
複利による運用を反対から考えたのが「割引現在価値」という概念です。
10,000円を5%で複利運用すると10年後に16,289円になるということは、逆に考えると将来10年後の16,289円は今の10,000円と同じ価値となるはずです。
これをEXCELの数式で表してみると次の通りになります。
※「^」キャップは〇乗を表す関数です。キーボード上の「半角傘マーク」がこれに当たります。
この式を次のように組み替えてみましょう。
10,000 = 16,289 / (1+5%)^10
更に組み替えて
10,000 = 16,289 × 1/((1+5%)^10)
この式の意味するところは、10,000円というのは、16,289円を年利5%、10年間の複利計算にて割り引いたものと同等になるということです。
この考え方を割引現在価値と言います。
割引率と複利現価率
逆に、将来10年後に5%を運用して10,000円となる現在価値を示すと次のようになります。
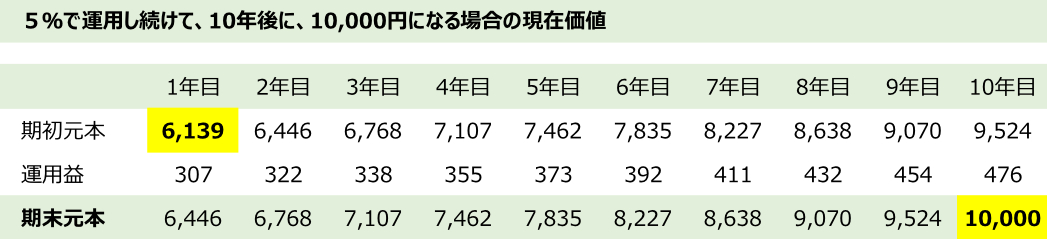
この場合の割引現在価値は6,139円になりますね。
割引現在価値を算出する際の、この5%を「割引率」と言います。
運用利回りと同じですね。
つまり次のような公式が成り立ちます。
( 1 /(1+割引率)^N)の部分を複利現価率と言います。
つまり、将来のおカネの価値に複利現価率を掛け算したものが、現在価値となるのです。
この割引現在価値の概念は、後に説明するDCF法を考えるに当たって非常に重要な考え方になります。
DCFとは、Discounted Cash Flowの略であり、このディスカウントとは正に「割引計算」を行うという趣旨になります。
不動産投資を例に具体例を見ていきましょう。
1,000のキャッシュフロー(CF)を生み出す不動産に投資したとしましょう。
この不動産の利回りを5%とすると、毎期のCFの現在価値は次のようになります。
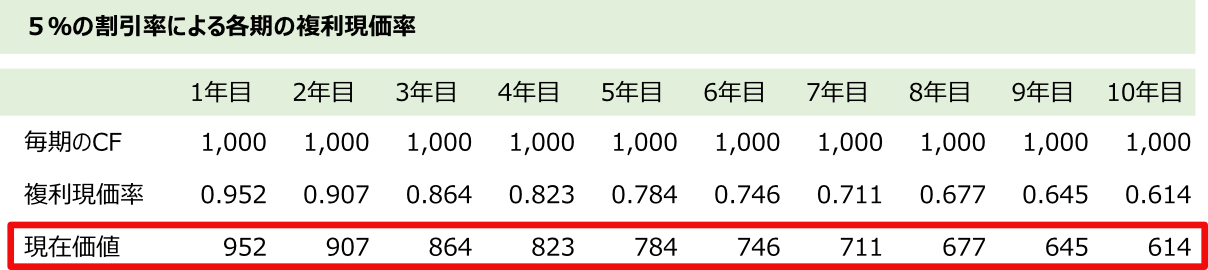
複利現価率が年を追うごとに小さくなり、現在価値も小さくなっていっていますね。
10年の投資期間の現在価値の合計は、7,722円となります。
つまり、10年間の投資期間のリターンの現在価値は7,722円となります。
ここでは、投資期間を10年としましたが、これを20年⇒30年⇒100年と計算した現在価値をグラフ化してみると次のようになります。
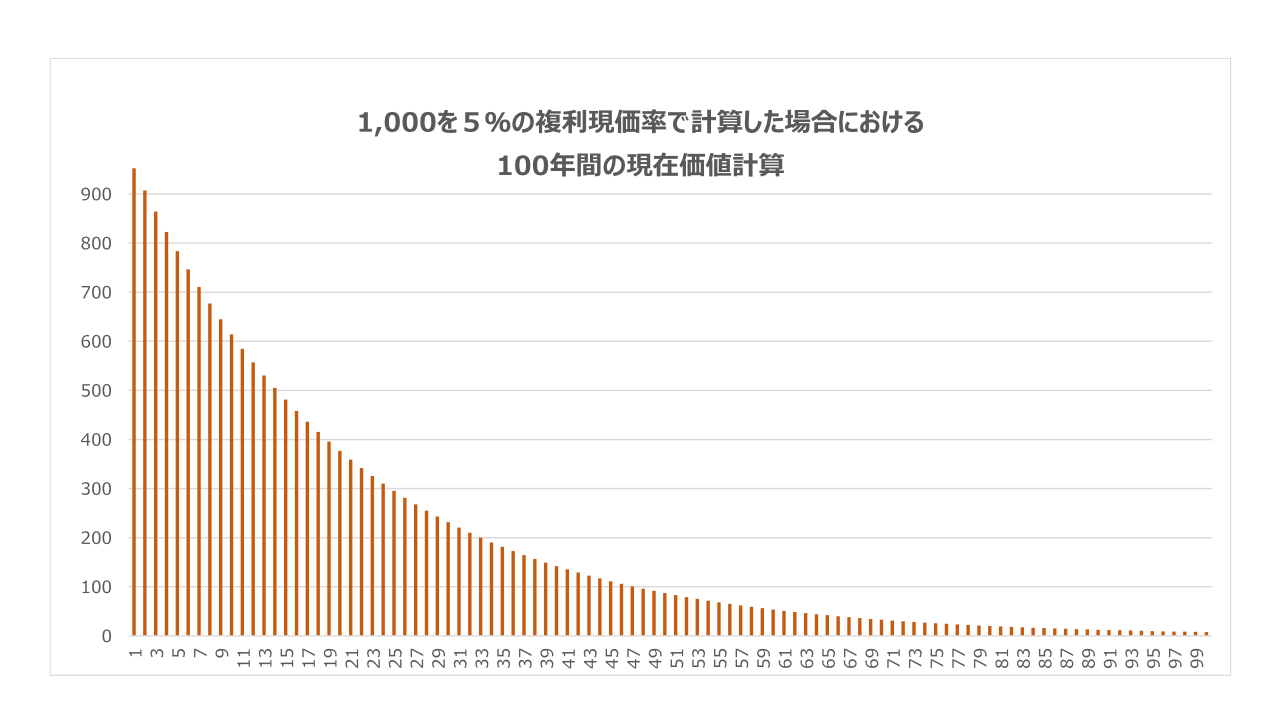
計算してみると、100年後の1,000の割引率5%による現在価値は、7.6と微々たるものになります。
更に、永久に計算していくと殆ど現在価値がゼロになるのは直観的に分かると思います。
そのように繰り返し無限大に計算していくと、現在価値の総額は次のような計算式と一致することになります。
1,000円÷5%=20,000円
毎期のCF÷還元利回り=収益価格の公式と一致することになります。
つまり、直接還元法による収益価格とは、毎期のCFの現在価値を無限に足し合わせたものと一致することになります。
直接還元法は別名、永久還元と言われるのはこのような理由からなのです。
この割引現在価値の考え方は、収益価格算定に当たって非常に重要なので、しっかり理解しておいてください。
次回は、収益還元法の2つの手法、直接還元法とDCF法についてそれぞれ概観してみましょう。
